Fraktale
Gelegentlich erzeuge ich in meiner Freizeit Fraktale mit selbstprogrammierter Software. Fraktale sind mathematisch präzise mit Hilfe zwei verschiedenen Arten von Dimension definiert (Topologische Dimension und Hausdorff-Dimension). Wir möchten hier aber nicht auf diese etwas abstrakte Definition eingehen (vielleicht schreibe ich in Zukunft einen längeren Abschnitt dazu). Fraktale sind häufig unendlich komplexe und auf verschiedene Weisen selbstähnliche geometrische Objekte. Selbstähnlich und unendlich komplex heisst, dass wir das Fraktal beliebig vergrössern können und immer wieder neue Strukturen vorfinden, die dem ganzen Fraktal ähneln. Dies ist auch für die Fraktale auf dieser Seite der Fall.
Ein typisches Beispiel für ein selbstähnliches Fraktal, das mit Computerprogrammen erzeugt werden kann, ist das Mandelbrot-Fraktal. Es ist nach Benoît Mandelbrot benannt, dem Vater der fraktalen Geometrie. Das folgende Bild zeigt eines der ersten Bilder, welches ich mit einer selbstprogrammierten Software erzeugte. Dargestellt ist ein Teil des Mandelbrot-Fraktals.
Alle meine Fraktal-Bilder in meinem flickr-album:
![]() Fraktale
Fraktale

Inhalt
Mandelbrot-Fraktal
Die Mandelbrot-Menge ist eine Untermenge der komplexen Zahlen. Vereinfacht kann man sich komplexe Zahlen wie zweidimensionale Zahlen vorstellen: Während gewöhnliche Zahlen (Reelle Zahlen) auf einer Linie aufgelistet werden können, müssen komplexe Zahlen in einer Fläche, der komplexen Ebene eingetragen werden. Jeder Pixel in einem Bild der Mandelbrot-Menge entspricht einer spezifischen komplexen Zahl.
Wir können für jede beliebige komplexe Zahl c bestimmen, ob sie Teil der Mandelbrot-Menge ist, indem wir die folgende Zahlenfolge betrachten:
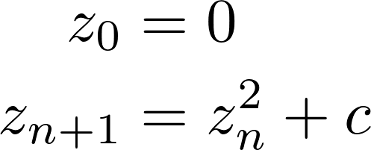
Alle Zahlen c, für welche die rekursive Folge divergiert, befinden sich nicht in der Mandelbrot-Menge. Die Zahlen der Mandelbrot-Menge sind demnach alle c, für welche die Folge beschränkt ist. Das Mandelbrot-Fraktal ist die Grenze zwischen den Zahlen, welche Teil der Menge sind und denen, welche ausserhalb liegen.
Es ist in der Regel unmöglich, mit Sicherheit zu bestimmen, ob die Folge für eine gegebene Zahl c divergiert, ohne unendlich Berechnungen durchzuführen; Wir begnügen uns daher mit einer Approximation: Wenn nach einer maximalen Anzahl Iterationen die Folge noch nicht divergierte, befindet sich die Zahl in der approximierten Mandelbrot-Menge. Je grösser die maximale Iterationszahl, desto genauer ist die Näherung und desto mehr Details kommen zum Vorschein.
Die Folge ist beschränkt, wenn die Magnituden aller z kleiner als 2 bleiben, denn sobald |z|>2, divergiert die Folge.
Die folgende Abbildung zeigt, wie die Mandelbrot-Menge relativ zur reellen und imaginären Achse positioniert ist.
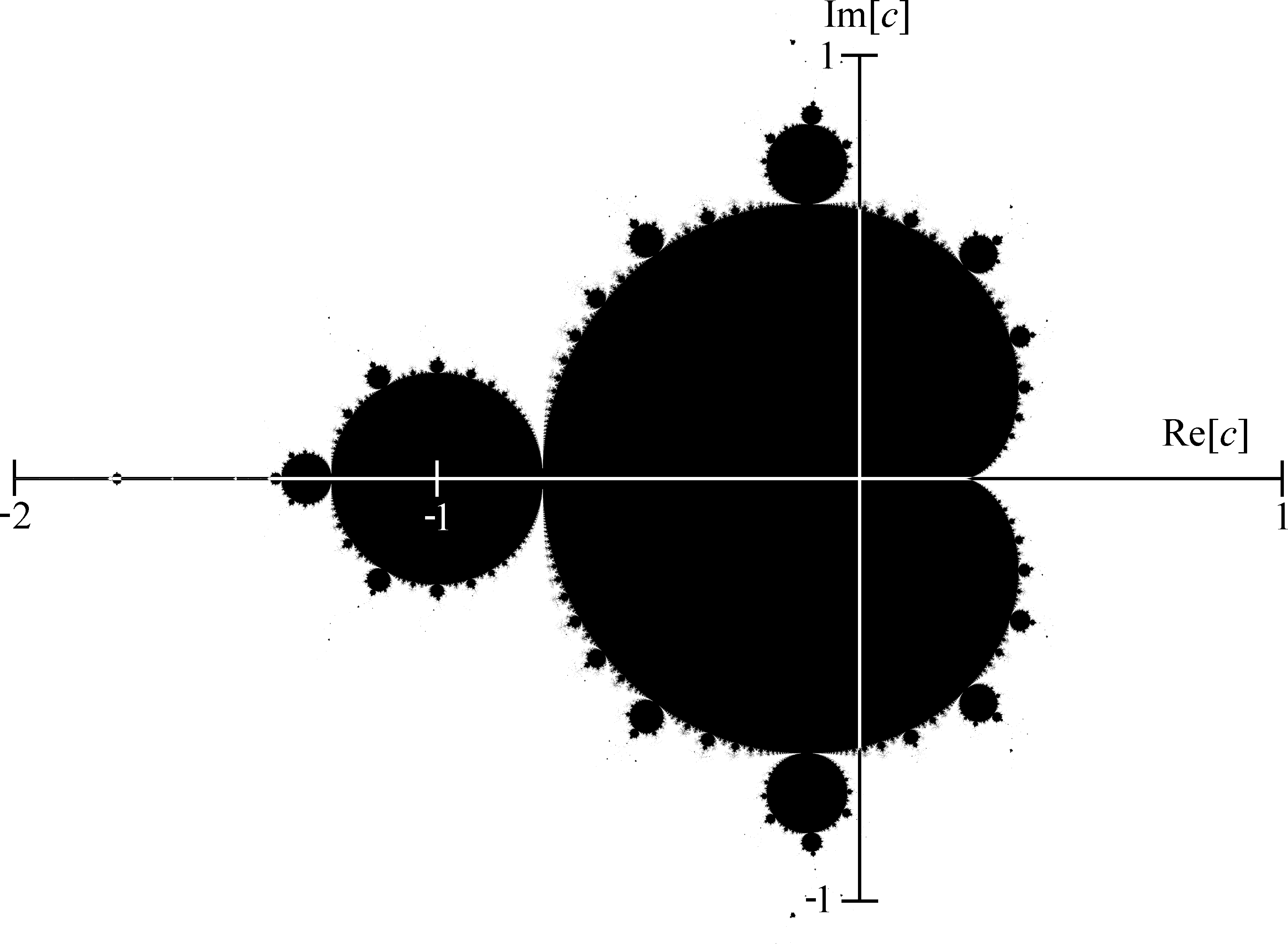
Um die Bilder der Menge ansprechender zu gestalten, können wir den Zahlen verschiedene Farben geben, je nachdem wie lange es dauerte, bis die Folge divergierte. Alle Zahlen, für welche die Folge nicht divergiert, werden schwarz eingefärbt.
Bilder
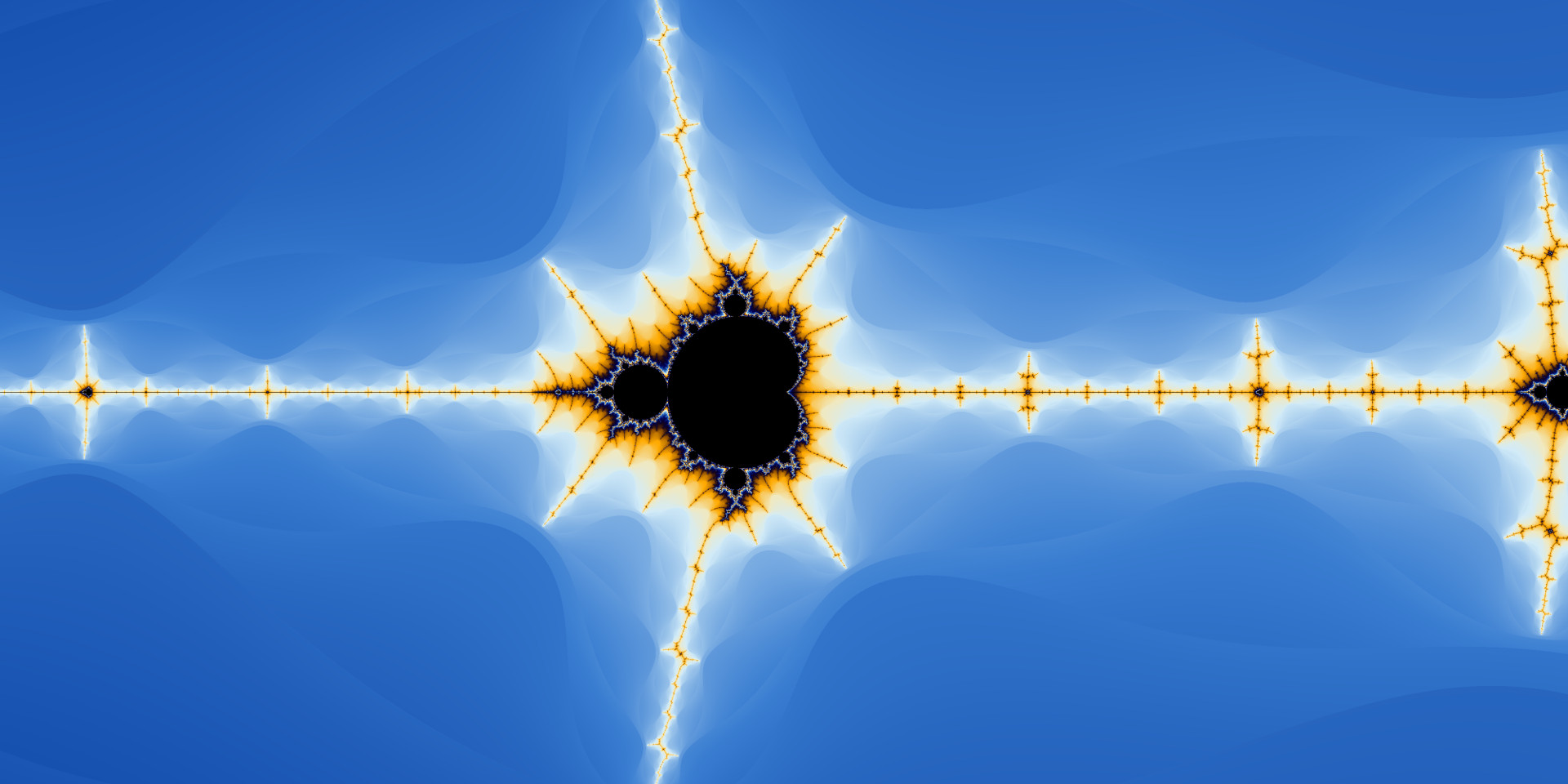
Die ersten beiden Bilder wurden mit meiner ursprünglichen, in C# geschriebenen Software erstellt. Später verbesserte ich diese, damit sie mittels Multithreading alle verfügbaren Prozessorkerne auslasten kann. Weil nun Bilder um ein Vielfaches schneller erzeugt werden konnten, begann ich die Auflösung der Bilder sowie die maximale Iterationszahl zu vergrössern. Die Software basiert auf Gleitkommazahlen mit doppelter Genauigkeit. Diese ermöglichen Zooms bis rund 1E-13. Die folgenden Bilder wurden alle mit der neuen Software erzeugt.



Das folgende Bild hat eine Auflösung von 10000 mal 10000 Pixel. Das Bild in voller Auflösung kann hier gefunden werden.

Das nächste Bild des Mandelbrot-Fraktals hat eine Auflösung von 19200 x 10800, das heisst 207 Megapixel. Das Bild in voller Auflösung kann hier abgerufen werden.

Copyright
Wenn nicht anders angegeben, ist der Inhalt dieser Webseite (sebastiengarmier.ch/fractals) durch die CC BY-SA 4.0-Lizenz geschützt:
© Copyright 2017-2024 durch Sébastien Garmier, sebastiengarmier.ch.