Physics Projects
list of publications
![]() Google Scholar
Google Scholar
Contents
ETH Master Thesis on Quantum Reference Frames
ETH Master Semester Project on Black Hole Information & Analogue Gravity
Activities in Analytical Mechanics (german)
ETH Bachelor Semester Project on the Shadow of a Rotating Black Hole
cuRRay - CUDA Relativistic Raytracer
ETH Master Thesis on Quantum Reference Frames
Short introduction coming soon!
title:
Transformations Between Imperfect Quantum Reference Frames
supervision:
Dr. Esteban Castro-Ruiz, LMF, Université Paris-Saclay, CNRS, ENS Paris-Saclay, France
Ladina Hausmann, institute of theoretical physics, ETH Zürich, Switzerland
Prof. Dr. Renato Renner, institute of theoretical physics, ETH Zürich, Switzerland
abstract:
Starting from the point of view of an observer, we provide a new construction for unitary
quantum reference frame transformations between observer perspectives, and under physical
assumptions derive the existence of an observer-independent, external view. The non-trivial
problem of reversibly transforming between physically relevant imperfect reference frames is
solved by embedding such frames in perfect ones. Thanks to this embedding, our approach
allows transforming into the perspective of an imperfect quantum reference frame, in a
way which is consistent with the rich information theory of such frames. We explore the
consequences of the embedding and explain the point of view of an observer whose frame is
imperfect. The findings are applied to imperfect reference frames for one-dimensional Galilei
transformations, in light of potential future applications in quantum gravity.
publication in ETH research collection:
doi:10.3929/ethz-b-000620796
PDF file:
![]() master thesis
master thesis
ETH Master Semester Project on Black Hole Information & Analogue Gravity
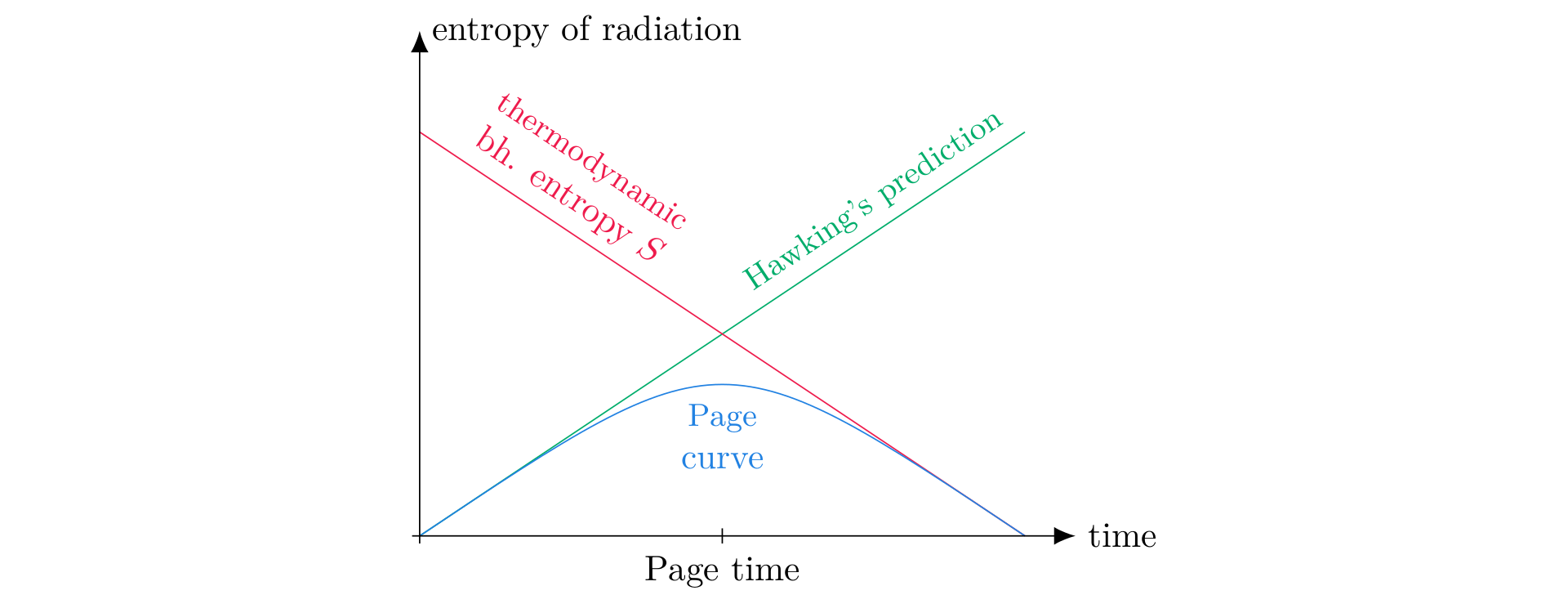
For my master in physics I wrote a semester project in theoretical physics on the black hole information loss paradox in the context of analogue gravity models. Roughly speaking, the information loss paradox is a contradiction between quantum field theory in curved spacetime and black hole thermodynamics: The former predicts that black holes lose mass through so-called Hawking radiation, and that the entropy of said radiation always increases. The latter says that the entropy of a black hole decreases as its mass decreases. For the two to be compatible, the entropy of the black hole must always be larger than that of the radiation. But the exact opposite happens.
Analogue gravity models are physical systems in which wave propagation mathematically resembles the propagation of a field (typically a massless scalar field) in curved spacetime. Thus, certain aspects of the system behave mathematically analogously to a field in curved spacetime. Interestingly, such analogue models can describe spacetimes of black holes, and one can even find Hawking radiation in those models. This leads to the question of whether the information loss paradox can also be described in analogue gravity models.
The goal of the semester project was to investigate this question: I argued that the analogy does not extend to the paradox, because black hole entropy has no useful analogy in the model. As a by-product, I developed a new approach to introducing a large class of analogue gravity models, including two of the most important ones.
title:
The Black Hole Information Loss Paradox in the Context of Analogue Gravity
supervision:
Giulia Mazzola, institute of theoretical physics, ETH Zürich, Switzerland
Prof. Dr. Renato Renner, institute of theoretical physics, ETH Zürich, Switzerland
abstract:
We investigate the possibility of approaching the black hole information loss paradox from the point of view of analogue gravity models. More generally, we ask whether analogue models can at all make inferences about gravity. To this end we give an intro-duction to black holes, the black hole information loss paradox, and analogue gravity models, before attempting to formulate the information loss paradox in the context of analogue gravity. We find that crucially, the notion of black hole entropy is missing, placing a discussion of the paradox in that context out of reach. Simultaneously, we argue based on the ubiquity and generality of analogue models that they are unlikely to possess deep connections with gravity.
PDF file:
![]() semester project
semester project
Activities in Analytical Mechanics (german)
This is a loose collection of independent activities in classical mechanics, special relativity, as well as Lagrangian and Hamiltonian mechanics. Each activity is provided with solutions, further comments and fitting literature.
The activities were create as part of my exercise class for the lecture Allgemeine Mechanik held by Prof. Dr. Renato Renner (institute of Theoretical Physics, ETH Zurich, Switzerland) in the fall semester of 2021.
For more information, see the german version of this page.
ETH Bachelor Semester Project on the Shadow of a Rotating Black Hole
In the last semester (spring 2021) of my BSc physics at ETH Zürich, I wrote a semester project in theoretical physics on the shadow of rotating black holes. The shadow of a black hole is the completely black area in the sky an observer sees when looking at an unobstructed black hole; the shape and size depends on the properties of the black hole and can even be used to infer some of these properties. The project is a literature review of fundamental as well as recent research in the field. As such, it can serve as a structured introduction to the field of black hole shadows.
Title:
The Shadow of a Rotating Black Hole
Supervision:
Prof. Dr. Philippe Jetzer (main supervisor), Physik-Institut, University of Zürich, Switzerland
Prof. Dr. Renato Renner (internal ETH member), Institute of Theoretical Physics, ETH Zürich, Switzerland
Abstract:
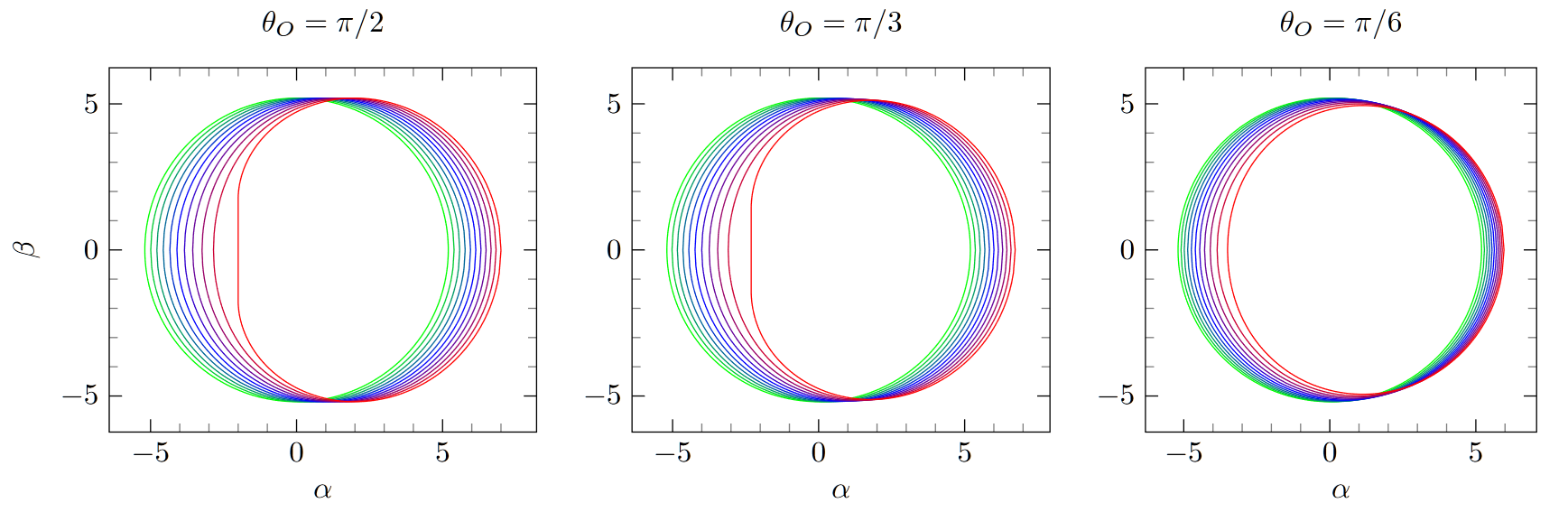
The aim of this work is to provide an introduction to the field of shadows of rotating Kerr black holes.
We review the mathematics of light propagation in Kerr spacetime and derive the equations describing the edge of a Kerr black hole shadow in the sky of a distant observer.
We also discuss recent research concerning the possibility of determining the spin parameter a and the inclination angle θO of the observer from direct observations of the shadow.
Finally, we showcase two applications of the theory of black hole shadows to the Event Horizon Telescope collaboration image of the supermassive black hole M87*.
PDF file:![]() semester project
semester project
The project can also be found on the webpage of Prof. Jetzer's research group: here.
cuRRay - CUDA Relativistic Raytracer
cuRRay is an acronym for CUDA relativistic raytracer, a software I programmed. The software calculates the trajectories of light particles, that is, light rays, near black holes. This way, images of objects near these cosmological monsters can be created. According to Einstein's theory of general relativity, light rays are deflected by the extreme gravity of black holes. The curved light rays lead to highly distorted images of the objects. cuRRay uses NVIDIA CUDA to efficiently compute the paths of light using the graphics card.
cuRRay is the software I programmed for my Matura project at my former high school, Kantonsschule Wohlen. The project won two main prizes at the 2018 swiss national contest of Schweizer Jugend Forscht (SJF): Firstly, a participation at the Stockholm International Youth Science Seminar (SIYSS) 2018, a week-long programme in the context of the Nobel prizes in Stockholm, Sweden. Secondly, a participation at the 2018 European Union Contest for Young Scientists (EUCYS) in Dublin, Ireland. There the project won a special price offered by the European Southern Observatory (ESO) allowing me to travel to Chile and visit telescopes and research sites of ESO. As a hobby astrophotographer, I particularely enjoyed this amazing trip.
You can find more information on cuRRay here.

Copyright
If not stated otherwise, all content on this website (sebastiengarmier.ch/physics) is protected by the CC BY-SA 4.0 license:
© Copyright 2017-2024 by Sébastien Garmier, sebastiengarmier.ch.